warum ist die wurzel aus drei irrational?
gute frage ha?
die richtige antwort (die, die ein normaler, sinnvoll denkender mensch geben würde):
wen interessierts?
die antwort, die ich bei meinem Studium geben soll:
Angenommen,  wäre rational. Dann könnte man die Zahl als Bruch zweier teilerfremder ganzer Zahlen a und b schreiben:
wäre rational. Dann könnte man die Zahl als Bruch zweier teilerfremder ganzer Zahlen a und b schreiben:
 .
.
Durch Quadrieren der Gleichung erhält man
bzw.
- 3b2 = a2 (1)
In Gleichung (1) ist die rechte Seite genau dann ungerade, wenn a ungerade ist. Ebenso ist die linke Seite (weil 3 ungerade ist) genau dann ungerade, wenn b ungerade ist. Folglich haben a und b die gleiche Parität. Als teilerfremde Zahlen können aber nicht beide gerade sein, also sind a und b beide ungerade. Demnach kann man sie mit geeigneten ganzen Zahlen m und n in der Form
- a = 2m + 1 bzw. b = 2n + 1
schreiben. Setzt man diese Ausdrücke in (1) ein, ergibt sich
- 3(4n2 + 4n + 1) = 4m2 + 4m + 1
und nach elementaren Umformungen (Ausmultiplizieren, variable Ausdrücke auf eine Seite bringen, Division durch 2)
- 1 = 2(m2 + m − 3n2 − 3n) (2)
In Gleichung (2) ist die rechte Seite gerade, da sie das Doppelte einer ganzen Zahl ist, während die 1 links ungerade ist. Dies ist ein Widerspruch, so dass die Annahme, 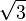 wäre rational, falsch sein muss. Folglich ist
wäre rational, falsch sein muss. Folglich ist 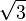 irrational.
irrational.
so, und jetzt von mir hier nochmal die frage: WEN INTERESSIERTS?
No Comments yet »
RSS feed for comments on this post. TrackBack URI


